Merkle Trees: Authentication, Integrity and Zero-Knowledge

Trees are a widely used data structure in computer science. From them emerges the Merkle tree, a simple yet very useful mutation of the basic tree concept. Originally developed by Ralph Merkle as a digital signature tool for ensuring data integrity and authentication, Merkle trees have become fundamental in cryptography and blockchain-related systems.

Definition

A Merkle tree is a data structure that, just like regular trees, can have different branching schemes. While it can be non-binary, its most common form is a binary tree.

To define it, we will see how it is constructed:

1. Leaves: Start with a list of elements (or data blocks). The leaves of the tree are created by hashing each individual element in the list.
2. Intermediate nodes: Next, create the parent nodes by hashing the concatenation of the hashes of the child nodes. This process continues recursively, building higher-level nodes until you reach the root.
3. Root: The last remaining node is the root of the tree, which serves as a cryptographic fingerprint of the entire data set.

Example: how to build a Merkle tree

Consider the following list: [d1, d2, d3, d4]. The + operation denotes the concatenation of hashes.

Authentication

When we want to prove that an element belongs to the Merkle tree, there is no need to check all the elements. Instead, we only need the element we want to authenticate and a sequence of hash concatenations that, starting from the given element, leads to the root of the Merkle tree. This sequence is called an authentication path or Merkle path.

To build this path, we navigate through the Merkle tree, starting from the hash of the relevant element and moving upwards. In each step, we record the hash concatenation that leads to each parent node, continuing until the root is reached.

Note that the recorded hash concatenations include only the hash corresponding to the element we are authenticating. The other hashes in the path are intermediate hashes in the tree, which are necessary for the verification but do not correspond to the elements themselves.

Example: how to obtain an authentication path

Consider the same list: [d1, d2, d3, d4]. To prove that d2 belongs to the list, we only need to provide d2 and its authentication path: [h(d1), h( h(d3) + h(d4) )]. With this information, anyone can calculate h(d2) using the public hash function and verify that the concatenations along the authentication path result in the public root hash. The only way for someone to provide an element x that builds up to the root hash is if that x is actually part of the list and located in the exact position specified by the authentication path.

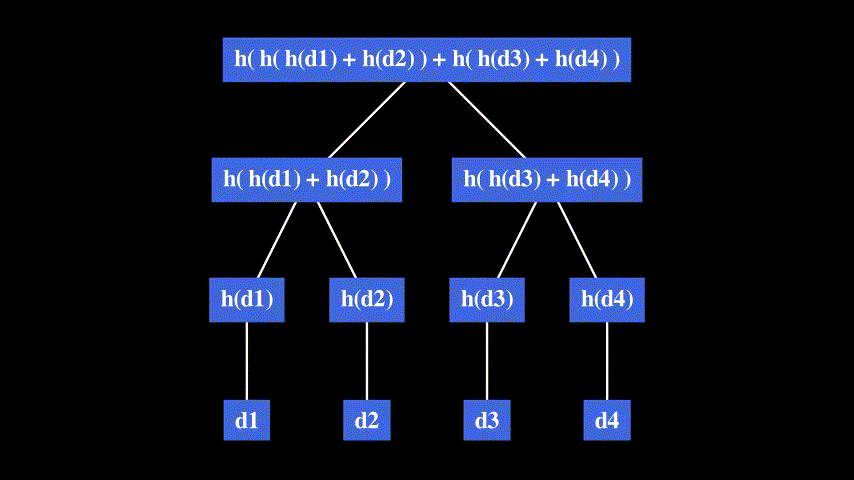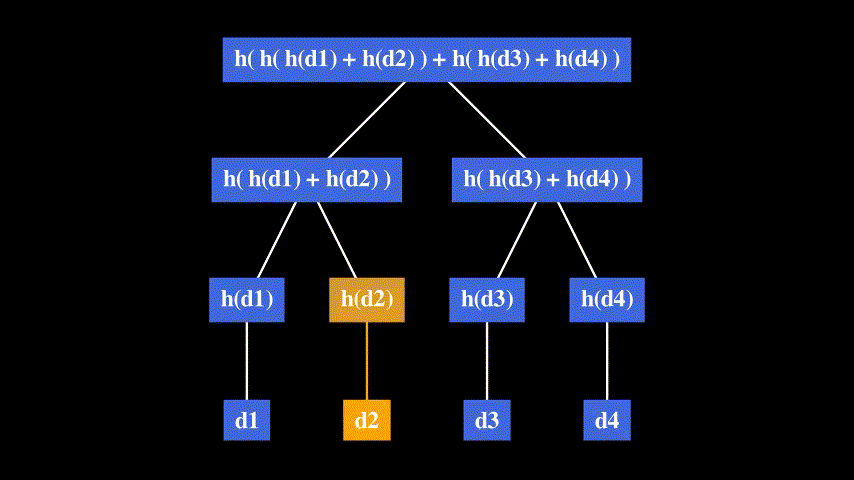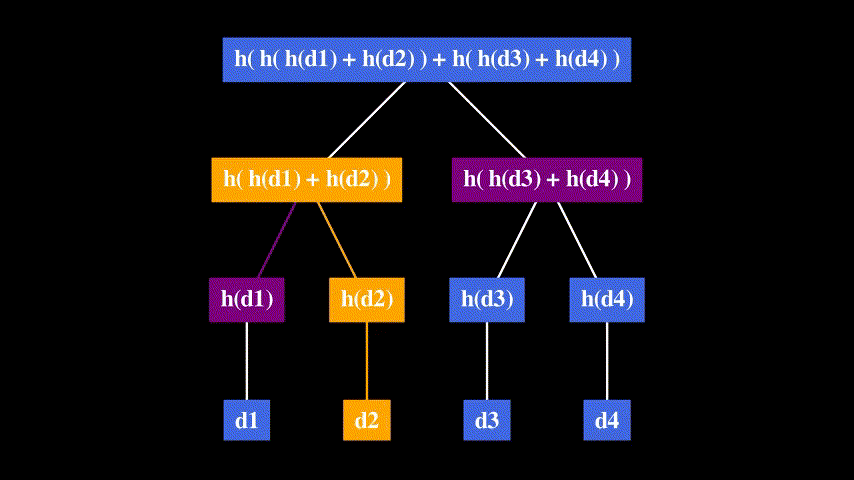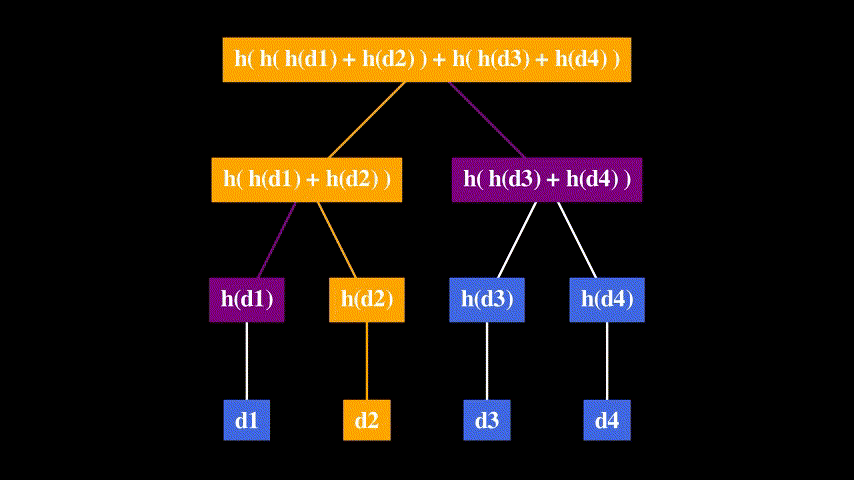
Take the root hash: h( h( h(d1) + h(d2) ) + h( h(d3) + h(d4) ) ), and the authentication path for d2: [h(d1), h( h(d3) + h(d4) )]. To authenticate d2, we calculate h(d2) with the public hash function and build the Merkle tree root hash from that using the authentication path.

Example: daily life use case

Take Alice, Bob, and Charlie, for instance. Alice is a credit agency that maintains people’s credit scores. Bob is a client of Charlie Bank and is applying for a loan. To process the loan, Charlie Bank needs to verify Bob’s credit score.

1. To ensure privacy, Alice constructs a Merkle tree from the list of credit scores and publishes only the root hash every week. This allows verification without revealing individual scores.
2. Bob, the rightful owner of his credit score, requests it from Alice.
3. Alice provides Bob with both his credit score and the corresponding authentication path. This path serves as proof that his score is included in the Merkle tree that corresponds to the publicly available root hash.
4. Bob then submits his credit score and the authentication path to Charlie Bank.
5. Charlie verifies that the provided authentication path correctly reconstructs the public root hash, confirming that Bob’s credit score is authentic and unchanged.

Through this exchange, Alice ensures that Bob can prove his credit score to Charlie Bank without exposing the entire credit score list to the public.

Main applications

Data integrity and authentication

• Preventing some of the risks present in peer-to-peer networks, like ill-intentioned parties altering information, or even simple data loss.
• Allowing for the distribution of information sources: receiving the highest part of the tree from a trusted source, and subsequent data from a closer, faster but untrusted source while also making sure that data was not altered.
• Commitment verification and secret-sharing in multi-party computation systems.

Efficient data synchronization

• Identifying which blocks of data should be updated in CDNs and distributed databases, and efficiently updating the root of the tree using the unmodified subtrees.

Zero-knowledge proofs

• Proving that a specific element is included in a private set, without revealing the whole set to the verifier.
• Proving that a specific element is excluded from a private set, without revealing the element to the verifier, using sparse Merkle trees.

Concrete applications

• A good explanation of the use of Merkle trees to optimize build systems is provided in this article on lwm.net.
• NixOS is a widely used operating system that implements Merkle trees for boot-time integrity checks, as mentioned here.
• Many cryptocurrency exchange platforms use Merkle trees as the foundation for their Proof of Reserves mechanisms, allowing them to prove that their funds cover users’ assets. Binance has their own article explaining it.
• The Early Detection Framework was proposed in this paper by researchers aiming to help optimistic rollups reduce verification costs and processing time.